Physics Processes¶

The standard RAT simulation includes many standard GEANT4 physics processes, as well as some custom processes:

Scintillation¶

(‘’‘DISCLAIMER’‘’: While the scintillation code in RAT is based on GLG4Sim by Glenn Horton-Smith, we have made several modifications to the code which change its behavior. Assume all bugs are ours!)

The scintillation simulation in RAT is handled differently than all other physics processes. In order to conserve energy on a step-by-step basis, scintillation photons are computed not as a standard GEANT4 physics process, but rather as a separate task after all other physics processes have run. The scintillation code can then look at the energy deposited during that completed step and calculate the number of scintillation photons that would be generated. A secondary task of the scintillation code is to handle reemission of photons in volumes which contain wavelength-shifter.

Code Structure¶

When the [source:rat/src/core/Gsim.cc Gsim::Init()] method is called, all of the GEANT4 user callbacks are established. One of these callbacks is the for a custom G4UserSteppingAction called [source:rat/src/core/GLG4SteppingAction GLG4SteppingAction]. At the end of each step, this class performs several tasks, among which is calling the static method [source:rat/src/core/GLG4Scint.cc GLG4Scint::GenericPostPostStepDoIt()]. GLG4Scint::!GenericPostPostStepDoIt() returns at G4VParticleChange object which contains the new secondary tracks (either scintillation photons or wavelength shifted photons) to be registered with the GEANT4 Stepping Manager.

In order to handle particle-specific scintillation parameters, a list of GLG4Scint objects are built by GLG4PhysicsList at startup, each responsible for a different particle. The static [source:rat/src/core/GLG4Scint.cc GLG4Scint::GenericPostPostStepDoIt()] method picks one of these objects based on the mass of the particle in the track. This list of particles is current limited to:

* (default)
* neutron
* alpha
* Ne20
* Ar39
* Ar40

If scintillation parameters are not specified for one of these particle types, the GLG4Scint object will load the default parameters instead. Once a suitable GLG4Scint object has been identified for the track, the GLG4Scint::!PostPostStepDoIt() method is called. The rest of this page describes what GLG4Scint::!PostPostStepDoIt() actually does.

Computing Number of Scintillation Photons¶

Normal particles (i.e. not optical photons) can deposit energy gradually in the medium through ionization and other processes. At the end of each track step, GLG4Scint determines the total deposited energy, ‘’dE’‘, and the step length, ‘’dx’‘. Then it applies Birk’s Law to compute the deposited energy after quenching:

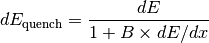
$dE_{\rm quench} = \frac{dE}{1 + B \times dE/dx}$

where ‘’B’’ is Birk’s Constant for your scintillator. If ‘’B’’ is set to zero, then Birk’s Law has no effect and the scintillator response is independent of ‘’dE/dx’‘.

An additional particle-dependent quenching factor, ‘’P(E)’’ can also be set which depends on the kinetic energy of the particle at the end of the step. This is useful if the scintillator quenching has been measured directly for a range of energies.

The deposited energy is converted to scintillation photons using the product of the light yield (‘’Y’‘) of the scintillator (which is in units of photons per MeV), the deposited energy, Birk’s Law scaling, the particle-dependent quenching, and a “reference ‘’dE/dx’‘” for Birk’s Law. The reference ‘’dE/dx’’ is useful if you have measured the light yield of the scintillator only with highly ionizing particles, like alphas, which already have a significant Birk’s Law component. The reference dE/dx effectively removes the quenching already in the light yield.

Finally, the mean number of photons can be scaled down by the “Photon Thinning” factor (‘’T’‘) selected by the user. Photon thinning is used to accelerate the simulation by reducing the number of optical photons produced by a constant factor, and then increasing the PMT photocathode efficiency by the same factor such that the product of light yield and detection efficiency is held constant.

Put together, the mean number of scintillation photons produced in the step is

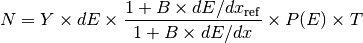
$N = Y \times dE \times \frac{1 + B \times dE/dx_{\rm ref}}{1 + B \times dE/dx} \times P(E) \times T$

Most of the factors in this equation are optional, and if not specified default to 1 for ‘’P(E)’’ and ‘’T’’ and 0 for ‘’B’’ and ‘’dE/dx_{ref}’‘.

The actual number of scintillation photons produced in the step is drawn from a Poisson distribution with mean N.

Scintillation Spectrum¶

Once the number of scintillation photons has been specified, the photon energy is drawn from a spectrum supplied for the material. The direction of each photon is randomly drawn from an isotropic distribution, and the polarization vector is randomly selected, but constrained to be orthogonal to the direction vector. The position of the photon is drawn from a uniform distribution along the line connecting the start and end points of the step.

Time Structure¶

The scintillation process has some time structure associated with it. The start time of a scintillation photon is the time the particle passed through the origin point of the photon, plus a delay drawn from the user-specified distribution. There are three possible options for the delay distribution:

A sampled time distribution, in the form of a list of (time, intensity) pairs.
A sum of decaying exponential distributions, each with an associated branching fraction and time constant.
A sum of two decaying exponential distributions, whose time constants are a function of particle energy.

The specification of delay distribution is described in the RATDB section below.

Wavelength Shifting¶

There are a few ways of doing bulk wavelength shifting in RAT. The default behavior is for GLG4Scint to handle opticalphotons as well as charged particles. Alternatively, you can also let GLG4Scint handle the primary scintillation, then use Geant4’s G4OpWLS process or the custom BNLOpWLSModel to do the reemission.

GLG4Scint Model¶

The previous sections only apply to particles other than optical photons. Optical photons are ignored by GLG4Scint, except when the photon is absorbed inside the medium, but not at a geometry boundary. If the photon is absorbed in the bulk, then it is possible that it was absorbed by wavelength-shifter present in the scintillator.

The decision whether to reemit the photon is made by looking at the REEMISSION_PROB table, which gives the Poisson mean number of photons number of photons produced per photon absorbed. (NOTE: This model is used because TPB shifts extreme UV light to visible light, so it is energetically possible for more than one photon to be produced. This model of reemission may not be applicable to all wavelength shifters.) The number of outgoing photons is drawn from this Poisson distribution.

The spectrum of the outgoing photons is drawn from a separate distribution from the primary scintillation distribution, unless no wavelength-shifting distribution is specified. In this case, the scintillation distribution is reused.

Wavelength shifted photons are delayed from their absorption time according to the same time distribution as the original scintillator. (WARNING: THIS IS ALMOST CERTAINLY WRONG FOR MEDIA WITH BOTH SCINTILLATOR AND WAVELENGTH SHIFTER. SHOULD FIX!)

G4OpWLS Model¶

Choose this model in the macro with:

/PhysicsList/setOpWLS g4

before calling initialize. See the Geant4 documentation for more details on the required material properties.

BNLOpWLS Model¶

Choose this model in the macro with:

/PhysicsList/setOpWLS bnl

This was written by L. Bignell at BNL to better model measurements of scintillator cocktails with secondary fluors. The reemission spectrum (and probability) is sampled depending on the photon wavelength, based on measured data. The file to read this data from is in RATDB, in BNL_WLS_MODEL[].data_path, which defaults to data/ExEmMatrix.root. The reemission time can be set to either a delta function or an exponential distribution, but currently is hard-coded to use an exponential. The latter is set through the property in the OPTICS table WLSTIMECONSTANT.

This model also requires OPTICS properties QUANTUMYIELD (vector, decides how many secondary photons to generate) and WLSCOMPONENT (vector, WLS wavelength intensity) for WLS materials.

This WLS model has been validated by Chao Zhang of BNL. See these slides for details: bnl_wls_validation.pdf.

RATDB Fields¶

This section needs work!

All of the RATDB fields which control scintillation are found in the OPTICS table for that material. The following table describes these parameters. Note that ‘’‘x’‘’ denotes a slot where a particle name (neutron,alpha,Ar40,Ar39,Ne20) which can be substituted in for particle-specific scintillation behavior. For example, one could create a field named SCINTILLATIONalpha_option. The default case would be written SCINTILLATION_option.

|| Name || Data type || Description || ||LIGHT_YIELD || double || Number of scintillation photons emitted per MeV of deposited energy || ||SCINTILLATION’‘’x’‘’_option || string || Units of SCINTILLATION’‘’x’‘’_value2. Always set to “dy_dwavelength”. || ||SCINTILLATION’‘’x’‘’_value1 || double array || List of wavelength points in nanometers. || ||SCINTILLATION’‘’x’‘’_value2 || double array || Relative number of emitted photons at each wavelength (integral is unimportant) || ||SCINTILLATION_WLS’‘’x’‘’_option || string || Units of SCINTILLATION’‘’x’‘’_value2. Always set to “dy_dwavelength”. || ||SCINTILLATION_WLS’‘’x’‘’_value1 || double array || List of wavelength points in nanometers. || ||SCINTILLATION_WLS’‘’x’‘’_value2 || double array || dN/dlambda at each wavelength (integral is unimportant) || ||SCINTMOD’‘’x’‘’ || double array || Three elements: [ 0.0d (always), Birk’s Constant, Reference ‘’dE/dx’‘]. || ||REEMISSION_PROB_option || string || Units of REEMISSION_PROB_value1. Always set to “wavelength”. || || REEMISSION_PROB_value1 || double array || List of wavelength points in nanometers. || || REEMISSION_PROB_value2 || double array || Mean number of reemitted photons for absorbed photon at that wavelength || ||QF’‘’x’‘’_option || string || Units of QF’‘’x’‘’_value1. Always set to “energy”. || ||QF’‘’x’‘’_value1 || double array || List of energy points in MeV || ||QF’‘’x’‘’_value2 || double array || Quenching factor at each energy point ||

The time delay for scintillation photons is controlled by SCINTWAVEFORM, LONGTIMECONST and ShortTIMECONST (note capitalization).

=== Case 1: Sampled time distribution ===

||SCINTWAVEFORM’‘’x’‘’_value1 || double array || List of time points in nanoseconds || ||SCINTWAVEFORM’‘’x’‘’_value2 || double array || dN/dt at each time (integral is unimportant) ||

=== Case 2: Sum of exponential distributions ===

||SCINTWAVEFORM’‘’x’‘’_value1 || double array || List of exponential time constants (in ns). All elements are negative. || ||SCINTWAVEFORM’‘’x’‘’_value2 || double array || Branching fraction for each time constant. Sum of elements must be equal to 1.0. ||

=== Case 3: Energy dependent, two exponential === || LONGTIMECONST’‘’x’‘’_option || string || Units of value1. Always set to “energy”.|| || LONGTIMECONST’‘’x’‘’_value1 || double array || List of energy points in MeV. Correspond to the current energy of the incident particle. || || LONGTIMECONST’‘’x’‘’_value2 || double array || Exponential time constant (ns) at each energy point. All elements are negative. || || ShortTIMECONST’‘’x’‘’_option || string || Units of value1. Always set to “energy”.|| || ShortTIMECONST’‘’x’‘’_value1 || double array || List of energy points in MeV || || ShortTIMECONST’‘’x’‘’_value2 || double array || Exponential time constant (ns) at each energy point. All elements are negative. || || LONGTIMEWEIGHT’‘’x’‘’_option || string || Units of value1. Always set to “energy”.|| || LONGTIMEWEIGHT’‘’x’‘’_value1 || double array || List of energy points in MeV || || LONGTIMEWEIGHT’‘’x’‘’_value2 || double array || Fraction of photons which are drawn from the long time constant at each energy. The fraction of photons drawn from the short time constant is (1 - this value).||

Note that all material property names (the names before _value1 and _value2) must be listed in the PROPERTY_LIST string array. (See examples for this to be more clear.)